HTTPS 可以保证我们的数据在传输过程中不被监听到,而按照之前的理解我们只是客户端通过公钥对数据进行了加密,随后由服务端通过私钥解密数据。但是这有一个很大的漏洞:服务端向客户端发送的数据如何防止被监听到?
前言
HTTPS 的加密机制虽然是个前端后端 ios 安卓等都应了解的基本问题,但网上的很多HTTPS相关文章也总会忽略一些内容,我学习它的时候也废了挺大功夫。
对称加密、非对称加密、数字签名、数字证书等等,在学习过程中,除了了解“它是什么”,你是否有想过“为什么是它”?我认为理解了后者才真正理解了HTTPS的加密机制。
本文以问题的形式逐步展开,一步步解开 HTTPS 的面纱,希望能帮助你彻底搞懂 HTTPS。特别是对于了解过 HTTPS 却在有些地方有所卡壳的人,希望本文能帮助你理清思路。
开始前先用一张图理清思路

为什么需要加密
因为 HTTP 的内容是明文传输的,明文数据会经过中间代理服务器、路由器、wifi 热点、通信服务运营商等多个物理节点,如果信息在传输过程中被劫持,传输的内容就完全暴露了,他还可以篡改传输的信息且不被双方察觉,这就是中间人攻击。所以我们才需要对信息进行加密。最简单容易理解的就是对称加密 。
对称加密
就是有一个密钥,它可以对一段内容加密,加密后只能用它才能解密看到原本的内容,和我们日常生活中用的钥匙作用差不多。
可行性
当然可行,但是前提是双方都能安全的拿到属于自己的密钥。可西出网关,谁又能一路让你畅通无阻把密钥安全送达?理论上来说其所经过的所有节点都可以对你所发送的信息进行监听,获取一方给另一方发送的密钥。而密钥一旦泄露加密自然也无从谈起。
当然你如果骨骼清奇,让浏览器里存下世界上所有 HTTPS 网站的密钥,那也不是不行对吧
既然无法通过对称加密进行传输,那么我们只好用到我们的主角:非对称加密
非对称加密
非对称加密思想描绘了这样的美好场景:你的手上有两个密钥(一对密钥),它们有一定的关联,但没有办法通过其中一个算出另外一个。你把一个密钥紧紧地攥在手里,永远不向别人公布(私钥);把另外一个发送给我,当然,发送给我的途中,所有的设备都知道了这个密钥(公钥)。之后我用公钥加密了数据,并发送给你,你却可以奇迹般地用私钥解密它。更神奇的是,中间所有的设备,居然都不能用公钥解开它!
数学魔术
先从一个故事讲起。
小时候我的同学小明给我表演过这样的魔术:让我任意想一个三位数,然后把这个三位数乘以91,最后把乘积的末尾三位告诉他。我想到了123这个数,乘以91得到了11193,接着我去掉两位只保留后三位,把193告诉了他。结果他很快地说出我心里想的数是123。
这个魔术的解法其实很简单:小明知道我的结果193后,再用193乘以11,得到了2123。而2123的末尾三位数,就是我的想的123。
原理也很简单,因为91乘以11等于1001,而任意一个三位数乘以1001,乘积的末尾三位一定等于它本身。我在进行了123 91操作后,小明进行了乘以11操作,即整个步骤为123 91 11 == 123 1001。而中间有一次去掉前两位仅保留后三位的操作(除以1000取余),看似丢失了信息量,实际上对结果毫无影响。其中的数学原理是:如果最后要对乘积取余,那么在事先对乘数取余不会对结果造成影响。
而我的同学小张即使听到了小明告诉我:把心里想的三位数乘以91,和我告诉小明:结果末尾三位是193,也没办法解开我心里想的数。
至此,这个魔术的所有步骤已然满足了非对称加密的全部要素。
假如小张长大了,考上大学的小张会知道上面得到91和193后,要做的其实是解一个方程:91 x mod 1000 = 193。有这样一个原理:ab互质,且a x mod b = c,那么a n x mod b = n c。这时他迅速地算出91 11 mod 1000 = 1,那么91 11 193 mod 1000 = 193。就是说11 * 193 mod 1000 = 123,一定等于我想的三位数。
上面这个魔术已经很接近想要的答案了。失败之处在于,通过91(公钥)还是可以很容易的得到11(私钥)和加密信息的解。
但是,只要这个解法的难度足够大,让全班同学都无法解出来,这个加密方法就可以很放心的使用了。
RSA算法
- 上面的数学魔术向我们展示了非对称加密的一些要素
- 运算过程是单向的:我们对123做了两次乘法再取余操作(如果是对称加密,对应的运算则是加密是一次乘法,解密是一次除法)
- 运算结果有其周期性:一个三位数不管乘以多少次1001,最后结果的末尾三位一定是它本身
- 加密的结果无法用公钥解开:加密是123乘以91取1000的余数得193,这时丢失了信息且无法直接用91还原
- 破解难度大:全班同学都无法解开这段信息(如果不会辗转相除法)
而 1977 年出现,并在 2002 年获图灵奖的 RSA 算法就真正做到了这些。
原理
在进入正题之前我们需要先了解两个概念:模 & 模逆元

- 首先,我们得到两个质数
p、q,比如是13和17,并求得N和M。N = p * q = 13 * 17 = 221M = (p - 1) * (q - 1) = (13 - 1) * (17 - 1) = 192
- 选择一个小于
M的整数a,求得a关于M的 模反元素(模逆元)b(模反元素存在,当且仅当a与M互质)- 鉴于这玩意儿看的比较绕所以我们解释一下:我们最终需要拿到的是这个
b。而其与a、M有以下关系 a - 1 ≡ b mod M- 也就是
a * b ≡ 1 mod M - 通俗一点理解,就是通过运算而来的
M、N满足:任意数a的i次方除以N取余数,会呈现一个长度为M的周期。 
- 鉴于这玩意儿看的比较绕所以我们解释一下:我们最终需要拿到的是这个
- 销毁
p和q的记录
如此我们即可得到公钥 (N, a),私钥 (N, b)。所以我们将私钥保留,公钥传递给加密通讯对象。
传输&解密
加密
现在我们通过一系列的操作得到了刚才所讲的公钥 & 私钥,所以现在我们就可以向另一方发送数据了。
举个例子,Client 端已知 Server 端的公钥(N, a),且想要发送信息 n (假设为123)给 Server 端,所以可以利用此公式
$$
n^e ≡ c (mod \quad N)
$$
将 n 加密为 c。然后 Client 将 c 发送给 Server 端
解密
而 Server 端接收到 Client 传给我们的 c 之后可以使用它的私钥 b 来解密
$$
c^b ≡ n (mod \quad N)
$$
解码的原理是如下两个公式
$$
c^b ≡ n^{a*b}(mod \quad N)
$$
$$
ab ≡ 1 (mod\quad (p-1)) \quad 且 \quad ab ≡ 1(mod \quad (q - 1))
$$
故由 费马小定理 可知
$$
n^{ab} ≡ n(mod \quad p) \quad 和 \quad n^{ab} ≡ n(mod \quad q)
$$
故
$$
n^{ab} ≡ n(mod \quad pq)
$$
Why it can
一定有人会疑惑为什么这种加密方式可以被应用于非对称加密。
其安全性在于,知道公钥 (N, a) 的情况下,想要得到私钥 (N, b),只需要解出 b 即可。而解出 b需要 a*b mod M = 1 这个小张的方程。但这一次,小张不知道 M 是多少了。想要知道 M,他必须通过 N(也就是221)来分解出13和17。即这个的破解难度等同于因式分解一个整数的难度。
1994年彼得·秀尔(Peter Shor)证明一台量子计算机可以在多项式时间内进行因数分解。假如量子计算机有朝一日可以成为一种可行的技术的话,那么秀尔的算法可以淘汰 RSA 和相关的衍生算法。(即依赖于分解大整数困难性的加密算法) 。
所以科技的进步就是重构的 deadline。
所以,现在人类的科技水平根本没有办法分解出一个2000位左右的大整数(整数分解难题)。所以,只要 N 够大,这套体系就足够安全。我们可以很快的生成两个1000位的质数,然后把它们乘起来,但是没有办法分解它。
缺点
虽然 RSA 加密算法作为目前最优秀的公钥方案之一,在发表三十多年的时间里,经历了各种攻击的考验,逐渐为人们接受。但是,也不是说 RSA 没有任何缺点。由于没有从理论上证明破译 RSA 的难度与大数分解难度的等价性。所以,RSA 的重大缺陷是无法从理论上把握它的保密性能如何。在实践上,RSA 也有一些缺点:
- 产生密钥很麻烦,受到素数产生技术的限制,因而难以做到一次一密;
- 分组长度太大,为保证安全性,n 至少也要 600 bits 以上,使运算代价很高,尤其是速度较慢。
HTTPS
上面我们讲到了其非对称加密机制,可以使得密钥持有方可以接收公钥持有方所发送的数据。所以为了保证双方都可以通过非对称加密方式进行信息交互,双方必须获取对方的公钥!
Client向Server端发送请求,Server端明文回应以自身的公钥Server Plubic KeyServer向Client端发送请求,Client端明文回应以自身的公钥Client Plubic Key
此后双方都通过对方的公钥加密发 req,以自己的私钥解密 res ,就可以解决掉我们之前的问题咯。
而在此基础上浏览器和服务器各建立连接后进行非对称传输事实上也是可以的。我们将长字符串转为 Unicode 并按照一定规律拆分,一段段的发送给对方事实上也是一种办法。但是最大的问题在介绍 RSA 算法时也已经被提出:太耗时。
对称加密
所以兜兜转又回到了最初的起点 —— 对称加密。
加密只是手段而非目的,所以既然非对称加密破解时间长、难度高,那么我们只用它来传输对称加密的密钥!
Client向Server端发送请求,Server端明文回应以自身的公钥Server Plubic KeyClient端通过Server Public Key将随机生成的密钥Symmetry Key加密并发送给服务端- 服务端通过自己的
Server Private Key解密完成后即可拿到我们的对称加密密钥Symmetry Key,此后即可进行对称加密。
但是仍存在问题
中间人攻击
你如何保证不会被 中间人攻击 ?
事实上我们在使用一些第三方插件进行 HTTPS 请求拦的思路正是如此。我们通过营造一个 “中间人” 的身份,在 Client 端扮演服务器,在 Server 端扮演浏览器,同样的自己生成两套公密钥不就完成了信息的拦截么?
证书机制
所以为了保证与我们交流信息的另一方的可信赖程度我们引入了证书机制
现实生活中,如果想证明某身份证号一定是小明的,怎么办?看身份证。这里政府机构起到了“公信”的作用,身份证是由它颁发的,它本身的权威可以对一个人的身份信息作出证明。互联网中能不能搞这么个公信机构呢?给网站颁发一个“身份证”?
我们此处讲的 证书(
digital certificate;public key certificate) 指的是 CA 证书,即,由 CA(Certificate Authority) 签发的,具有公信力的,可以证明网站身份的凭证。只有由 CA 签发的证书才具有公信力,而与此同时证书还有一个信任链,由根证书起向下延伸。就好比如今的互联网一线大厂寻找的外包商往往也是行业内的技术翘楚,踏实可靠,值得信赖。如此一级信任一级就组成了我们所说的证书信任链,这些我们后边再讲
我们把证书内容生成一份“签名”,比对证书内容和签名是否一致就能察觉是否被篡改。这种技术就叫数字签名
数字签名
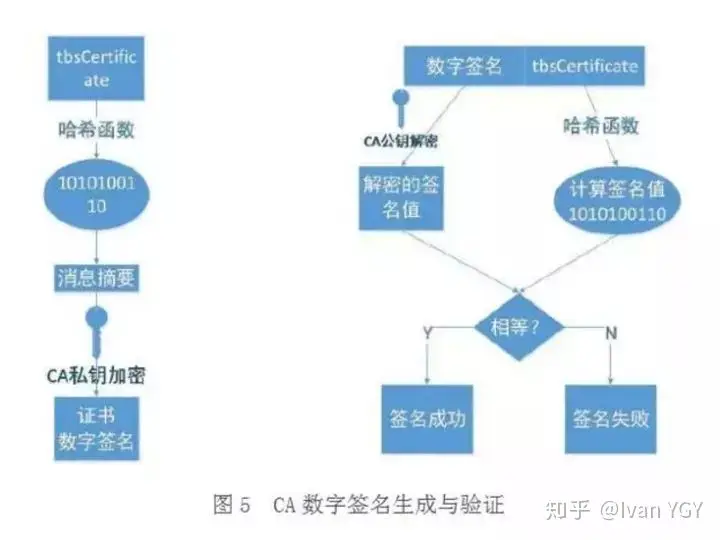
制作过程
- CA 拥有非对称加密的私钥和公钥。
- CA 对证书明文信息进行hash。
- 对 hash 后的值用私钥加密,得到数字签名。
明文和数字签名共同组成了数字证书,这样一份数字证书就可以颁发给网站了。
那浏览器拿到服务器传来的数字证书后,如何验证它是不是真的?(有没有被篡改、掉包)
验证过程
- 拿到证书,得到明文 T,数字签名 S。
- 用 CA 机构的公钥对S解密(由于是浏览器信任的机构,所以浏览器保有它的公钥。详情见下文),得到 S’。
- 用证书里说明的 hash 算法对明文 T 进行 hash 得到 T’。
- 比较 S’ 是否等于 T’,等于则表明证书可信。
为什么这样可以证明证书可信呢?我们来仔细想一下。

首先,服务器端需要先向CA机构申请证书,申请证书的时候,服务器向CA机构提供服务器的公钥,CA机构用自己的CA私钥对服务器的公钥进行签名,生成数字摘要,然后将服务器公钥和数字签名打进证书。
客户端从服务器拿到证书后,根据证书上的CA签发机构,从内置的根证书里找到对应的CA机构公钥,用此公钥解开数字签名,得到摘要,根据此验证证书的合法性。
结合另一张图进行证书机制的理解

杂记
证书
证书内部包含了发布者的公钥(Public Key)、数字签名(tbsCertificate)、以及相应网站的信息。
如此一来假设中间人篡改了证书原文,由于我们无 CA私钥 故无法得到加密后签名,无法通过浏览器验证,故无法操作。另一方面,由于证书中包含了网站的基本信息,所以浏览器只需将证书信息中域名与自己请求的域名进行对比即可知证书是否被整个掉包,故这方面也没有操作空间。
根证书
操作系统、浏览器本身会预装一些它们信任的根证书,如果其中有该CA机构的根证书,那就可以拿到它对应的可信公钥了。
证书之间的认证也可以不止一层,可以A信任B,B信任C,以此类推,我们把它叫做信任链或数字证书链,也就是一连串的数字证书,由根证书为起点,透过层层信任,使终端实体证书的持有者可以获得转授的信任,以证明身份。
另外,不知你们是否遇到过网站访问不了、提示要安装证书的情况?这里安装的就是跟证书。说明浏览器不认给这个网站颁发证书的机构,那么没有该机构的根证书,你就得手动下载安装(风险自己承担XD)。安装该机构的根证书后,你就有了它的公钥,就可以用它验证服务器发来的证书是否可信了。
HTTPS&TSL握手
显然每次请求都经历一次 TSL 握手和密钥传输过程都非常耗时,那怎么达到只传输一次呢?用 Session 就行。
服务器会为每个浏览器(或客户端软件)维护一个 Session ID,在 TSL 握手阶段传给浏览器,浏览器生成好密钥传给服务器后,服务器会把该密钥存到相应的 Session ID 下,之后浏览器每次请求都会携带 Session ID,服务器会根据 Session ID 找到相应的密钥并进行解密加密操作,这样就不必要每次重新制作、传输密钥了!
具体细节可以参考我的另一篇文章 《带你了解Cookie、Session和Token》
制作数字签名时的hash
似乎以上过程中hash有点多余,把hash过程去掉也能保证证书没有被篡改。
最显然的是性能问题,前面我们已经说了非对称加密效率较差,证书信息一般较长,比较耗时。而 hash 后得到的是固定长度的信息(比如用md5算法hash后可以得到固定的128位的值),这样加密解密就会快很多。
当然还有安全上的原因,这部分内容相对深一些,感兴趣的可以看这篇解答:crypto.stackexchange.com/a/12780
归纳
最后我们用开始的那张图来对 HTTPS 握手过程进行总结

我们举个粗俗的例子,黄海波老师嫖娼。在此例子中黄老师扮演的是 Server,而在宾馆里给黄老师打电话的暗娼则是 Client。
- 1 ~ 2 部分就像是 小姐 对 客户 的要求 —— a(不能有过分的玩法)、b(不能有身体疾病)
- 2 ~ 3 部分则是黄老师给的回应 —— a(HHB 身体健康,无怪癖)、b(我的身份证,证明我就是 HHB)
- 而
客户端 - 服务端 - 客户端 - 服务端这三条线路所连接的过程就是我们的 TSL 握手过程,三次握手结束过后即可建立起双向非对称通信,也是我们所需要的可靠通路 - 随后 浏览器、服务器双方通过这三个伪随机数(计算机生成的随机数本质上都是伪随机数)生成一个真随机数,并以相同的算法共同计算得出对称加密的密钥。
- 至此,对称密钥传输完成,切换至对称加密,TSL 所建立的双向非对称通信通路彻底废弃。
总结
可以看下这张图,梳理一下整个流程(SSL、TSL握手有一些区别,不同版本间也有区别,不过大致过程就是这样):
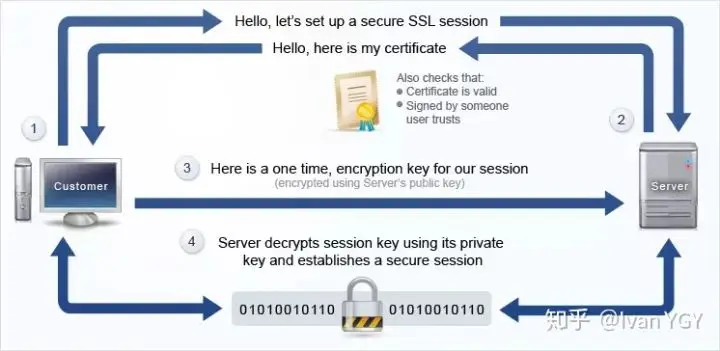
(出处:http://www.extremetech.com)
参考文章
- 《轻松学习RSA加密算法原理》
- 《彻底搞懂HTTPS的加密机制》
- 《非对称加密与HTTPS》
- 《模逆元》
- 《费马小定理》
- crypto.stackexchange.com/a/12780
- 《数字证书与数字签名》
由衷感谢参考文章列表中的各位大佬,并对黄海波老师献上最真挚的道歉和祝福。
